引入计算图
如下计算图是为$e=(a+b)(b+1)$.我们可以为节点$a$&节点$b$赋值来计算$e$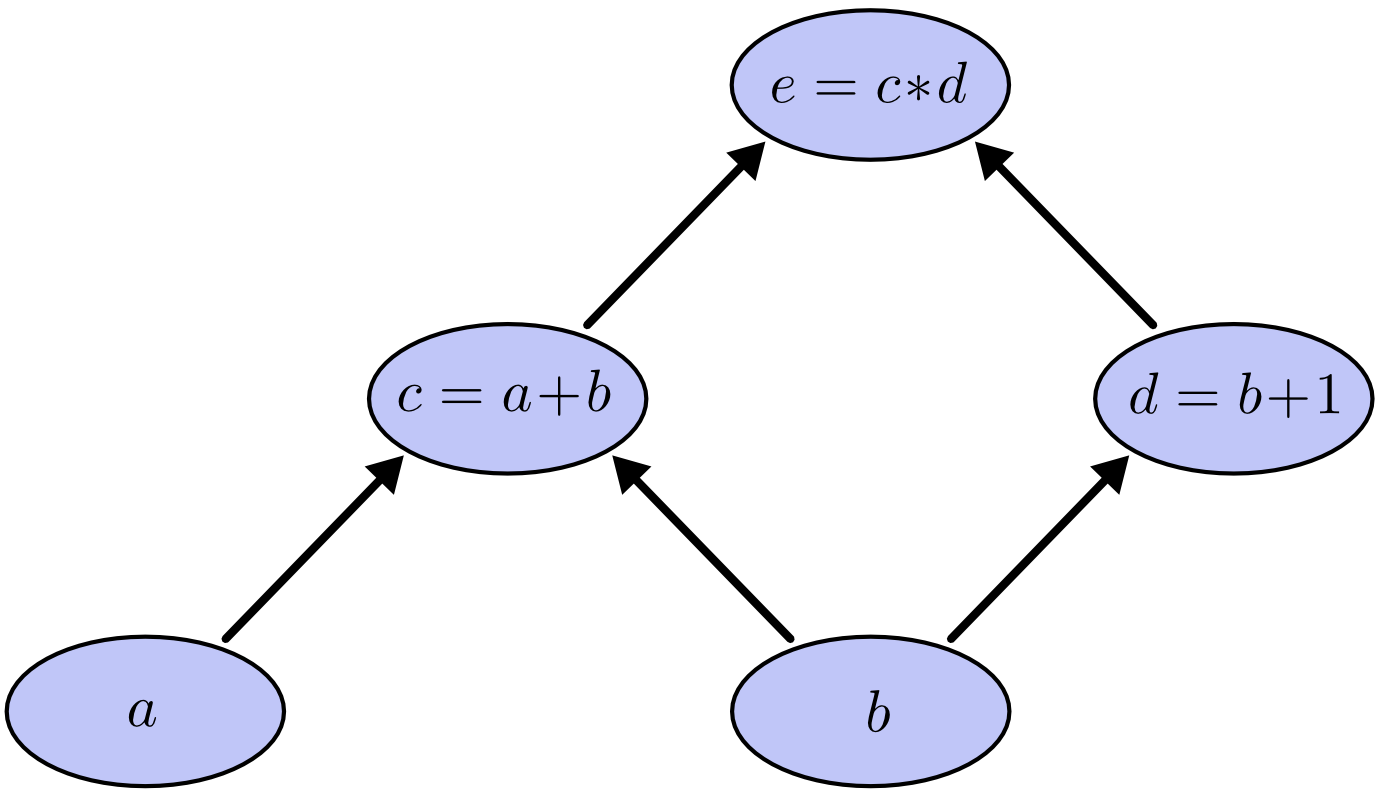
Factoring Path(路径因式分解)
考虑对下图的链式法则: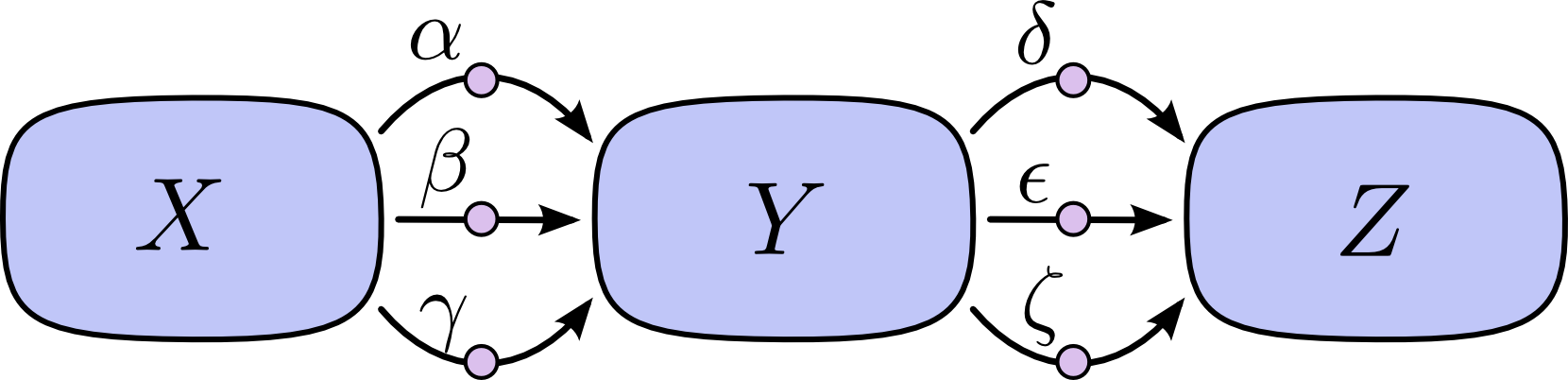
如果我们想要计算出$\frac{\partial Z}{\partial X}$,则必须要计算$3*3=9$条路径:
$$
\frac{\partial Z}{\partial X} = \alpha\delta + \alpha\epsilon + \alpha\zeta + \beta\delta + \beta\epsilon + \beta\zeta + \gamma\delta + \gamma\epsilon + \gamma\zeta(1)
$$
对上式进行因式分解则有:
$$
\frac{\partial Z}{\partial X} = (\alpha + \beta + \gamma)(\delta + \epsilon + \zeta) (2)
$$
公式(2)引出了“前向求导”和“反向求导”:它们都通过因式分解来高效计算偏导数。
前向求导
通过对每个节点上的路径的输入求和,我们可以得到总路径上的每个输入“影响”节点的偏导数。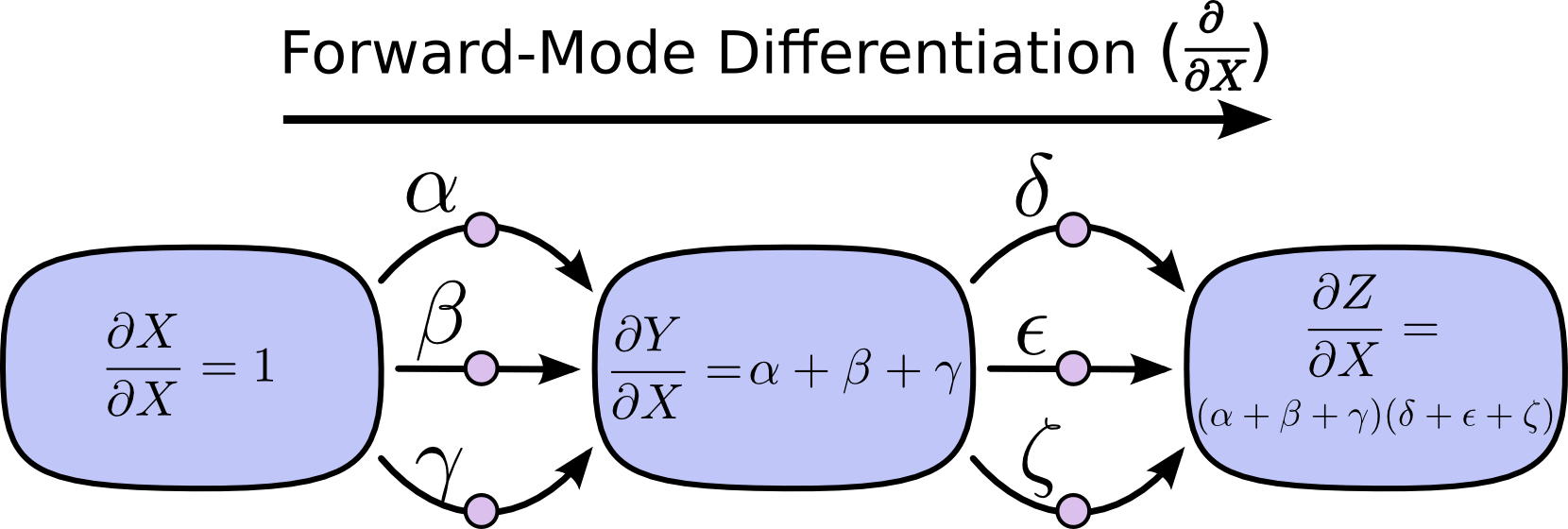
反向求导
从计算图的输出节点出发,向初始节点移动并且在每个节点处合并从该节点引出的所有路径:
前向求导和反向求导的对比
- 前向求导:跟踪每个输入如何影响所有节点,需要计算每个节点的$\frac{\partial}{\partial X}$。
- 反向求导:跟踪所有节点如何影响一个输出,需要计算每个节点的$\frac{\partial Z}{\partial}$。
计算速度的提升
如果对计算图的每条边添加偏导数则有: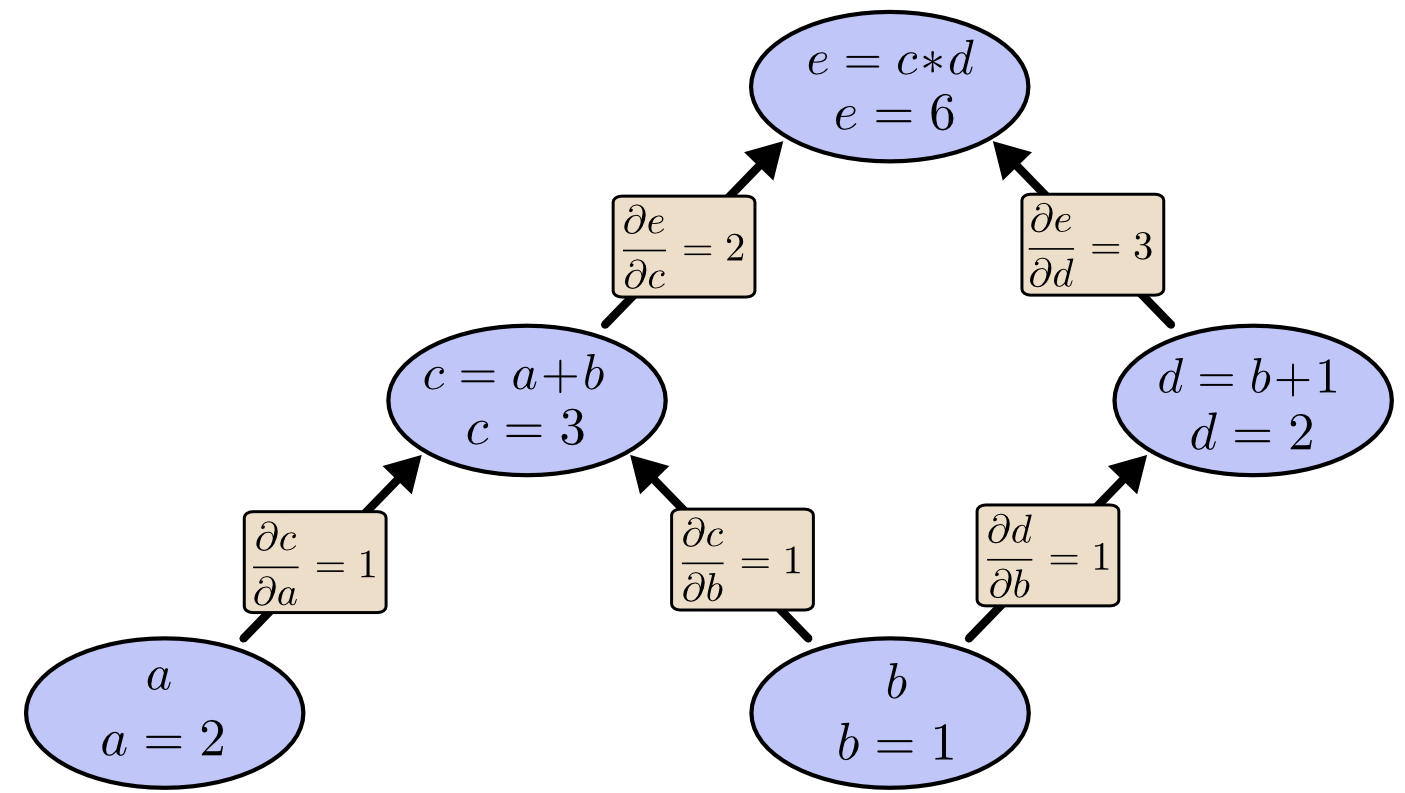
当我们使用前向求导来计算每个节点对$b$的偏导数则有:
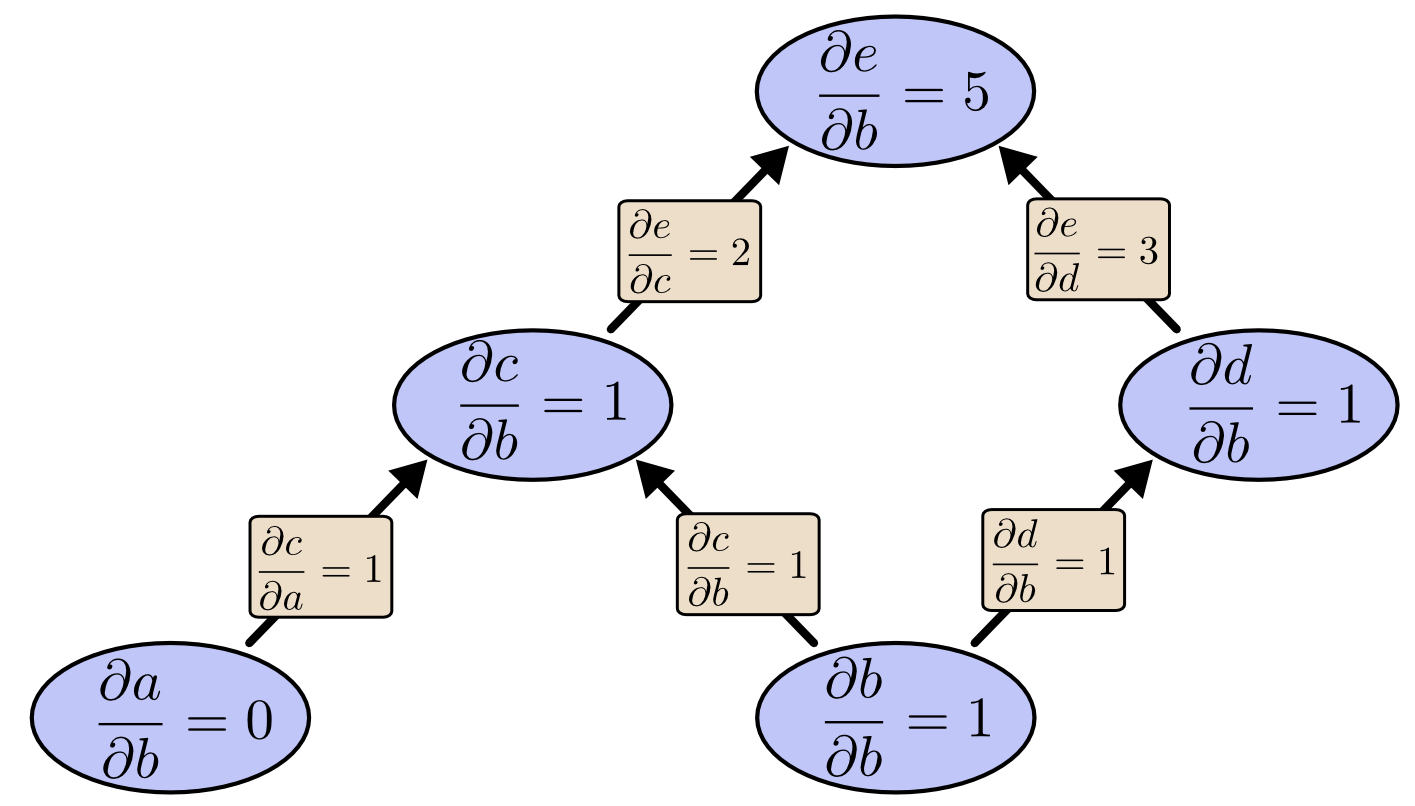
由上图可见计算出$\frac{\partial e}{\partial b}$的代价是需要计算很多“无用”的偏导数。[注:“无用”是因为在梯度下降的过程中,我们只关心输出对每个节点的偏导数]当我们使用反向求导计算$e$对各个节点的偏导数有:
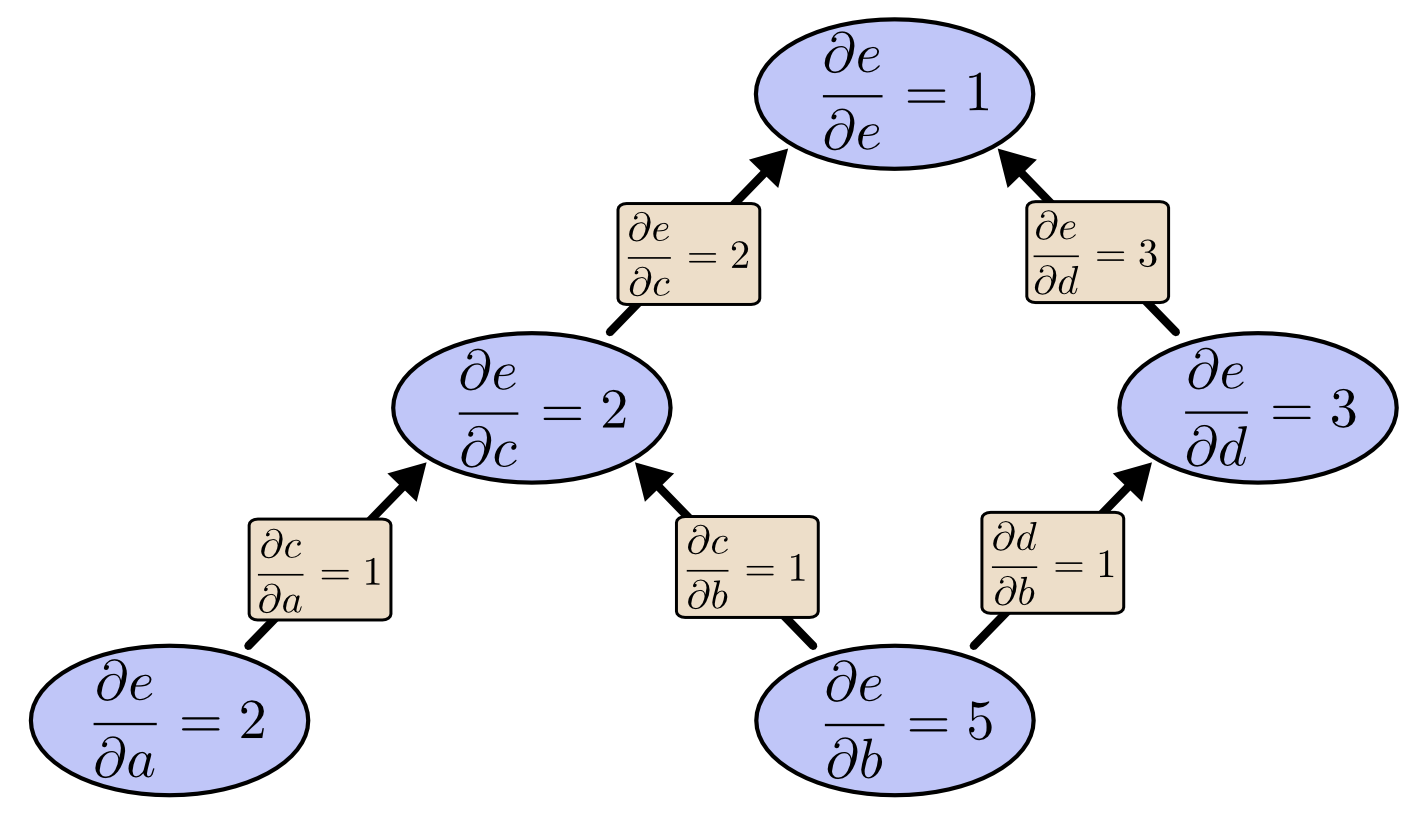
对比两张图可以发现,反向求导“真正”的给出了我们想要的偏导数。在有百万级别的输入时的极端情况下,前向求导需要计算百万次才能得到输出结果对所有节点的偏导数。而反向求导只需要计算一次。
在我们训练神经网络的时候需要计算对所有参数的偏导数用以梯度下降,因此反向求导极大的提升了计算速度。
Once you’ve framed the question, the hardest work is already done

